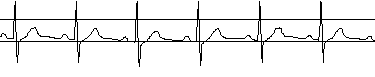
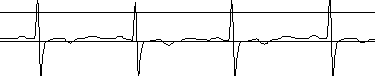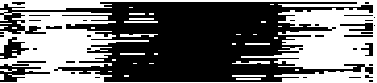Рис. 1. –ЭКС и соответствующий ему амплитудный спектр Фурье здорового человека (а); и ЭКС и человека с экстрасистолическим ритмом по типу тригеминии (б)
Форма нижней границы a(t) не зависит от t, то есть от длительности интервала R-R, поэтому спектр Ci ЭКС x(t) в нестационарном базисе
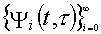
с единичным весом может быть вычислен как [3]
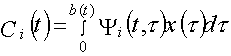 ,(1)
,(1)
тогда как спектр интервалов R-R Di(t) с точностью до мультипликативной составляющей вычисляется как
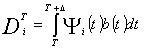 .(2)
.(2)

Рис. 2. Формирование нестационарных отрезков интервалов R-R
Верхний индекс Т показывает, что i-ая спектральная составляющая зависит от выбранного момента наблюдения сигнала. Апертура D также определяет величину
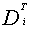 .
.
Однако при идентификации сигналов всегда можно договориться, что они были получены на апертурах равной длины. К сожалению, синхронизация по началу момента наблюдения ЭКС Т не дает положительного эффекта, что связано с нелинейным характером течения времени в организме.
На рис. 3 а,б приведены спектрограммы ЭКС одного и того же пациента, полученные согласно (2) при D=5 минут при Т1=13 часов 50 минут (а) и Т2 = 4 часа 5 минут (б).
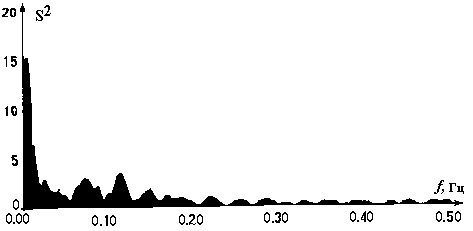
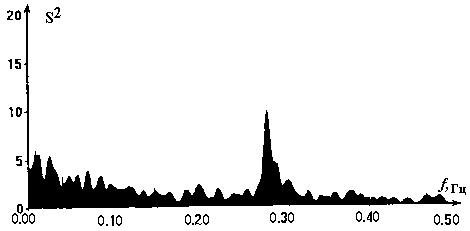
Рис.3. Спектрограммы R-R интервалов одного и того же пациента, полученные в разные моменту времени на одной и той же апертуре наблюдения
Исходя из этих спектрограмм, для каждого момента Т могут быть выделены некоторые ритмы, привязанные к анатомическим и физиологическим характеристикам объекта. В литературе описано достаточно много таких ритмов: это волны Майера, Траубе-Геринга, дыхательные ритмы , ритмы 2Т и т.д. На спектрограммах, показанных на рис.3, можно выделить эти ритмы и при определении интеграла (1) в качестве верхнего предела использовать соответствующий период ритма. Учитывая, что левая часть (1) является непрерывной функцией t, то подставляя в правую часть (1) в качестве верхнего предела интегрирования конкретные значения периодов ведущих ритмов, получаем матрицу спектральных коэффициентов, число строк которой определяется числом ведущих ритмов, а число столбцов – числом спектральных коэффициентов, используемых в разложении. Полученную матрицу назовем разложением сигнала по m собственным ритмам в нестационарном ортогональном базисе
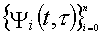 .
.
Основным критерием эффективности любого унитарного преобразования является его способность адекватно описывать исследуемый процесс в пространстве меньшей размерности, чем пространство исходного сигнала. В данном случае это не имеет место по той причине, что ряд ритмов слабо коррелированны, а другие ритмы неустойчивы [4]. С другой стороны, имеют место ритмы, между которыми существует однозначная связь, например, предсердные и желудочковые осцилляторы. Поэтому целесообразно из совокупности ритмов, определяемых спектральными коэффициентами 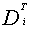 выбрать наиболее коррелированные ритмы. Очевидно, что наиболее коррелирован ритм сам с собой, поэтому в качестве нестационарных отрезков, на которых определяются спектральные коэффициенты, могут быть взяты отрезки, определяемые одним и тем же ведущим ритмом, назовем такое разложение сингулярным разложением по собственным ритмам в базисе нестационарных ортогональных функций
выбрать наиболее коррелированные ритмы. Очевидно, что наиболее коррелирован ритм сам с собой, поэтому в качестве нестационарных отрезков, на которых определяются спектральные коэффициенты, могут быть взяты отрезки, определяемые одним и тем же ведущим ритмом, назовем такое разложение сингулярным разложением по собственным ритмам в базисе нестационарных ортогональных функций
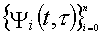 .
.
В этом случае мы привязаны к одному “ритмическому” масштабу в строках матрицы сингулярного разложения, поэтому можем утверждать, что двигаясь по столбцам этой матрицы мы имеем дело с одним и тем же “ритмическим” масштабом несмотря на нестационарность интервала разложения и таким образом каждый столбец нестационарной сингулярной матрицы описывает процесс эволюции ритмов ведущего ритма по первой координате времени t, в то время как строки сингулярной матрицы описывали спектр исходного сигнала x(t) по второй координате времени t. Очевидно, что в случае стационарного процесса x(t) после определения спектра столбцов сингулярной нестационарной матрицы мы получаем матрицу, элементы которой отличны от нуля только в первой строке. При наличии нестационарности появляются дополнительные элементы, отличные от нуля. Исследуя спектр b(t) (рис. 3), можно выбрать ведущий ритм сингулярного нестационарного разложения таким образом, чтобы в спектре нестационарной сингулярной матрицы было максимальное число нулевых элементов, или в первой строке матрицы спектра сингулярной матрицы была сосредоточена максимальная мощность.
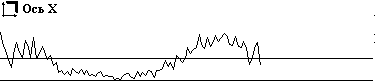
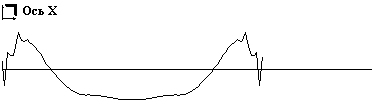
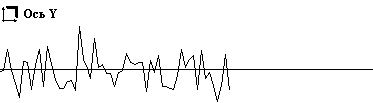
В качестве примера сингулярного разложения на нестационарных отрезках собственных частот на рис. 4 приведены сингулярные матрицы ЭКС. Так как в качестве способа визуализации матриц выбрано полутоновое изображение, то каждая матрица на рисунке представлена двумя изображениями. На изображениях справа визуализируются все элементы матрицы. При этом практически вся энергия спектра сосредоточена в первой строке матрицы, поэтому на изображении, по существу, представлена одна строка. На изображении слава первая строка исключена, что позволило эмулировать режим "лупы". Под каждым изображением показаны сечения сингулярной матрицы по осям Х и Y.
Исследования сингулярных матриц ЭКС, проведенные нами показали, что первая строка матрицы достаточно адекватно описывает его тривиальное спектральное разложение, которое представленным способом получается значительно быстрее, при этом в качестве информативных признаков могут использоваться первые шесть – восемь гармоник. В последующих строках идет селекция энергии ЭКС по ритмам верхней иерархии или гармоническим составляющим этих ритмов. Тогда задача принятия решения сводится к выбору ритма/ритмов верхней иерархии, которые коррелированны с исследуемой патологией или анатомическим органом. Таким способом достигается сокращение пространства признаков, например, можно вместо всей сингулярной матрицы рассматривать только одно ее сечение по оси Х, показанное на рис. 4. Однако использование такого способа сокращения пространства признаков требует его испытания в клинических условиях, то есть получения атласа сингулярных матриц ЭКС.


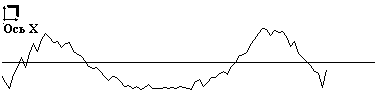
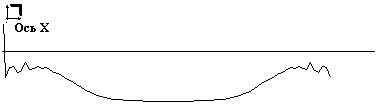
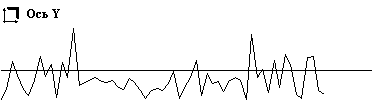

а)
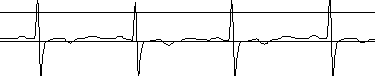
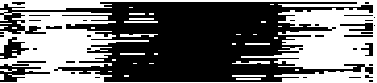

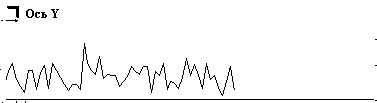
б)
Рис. 4. Матрицы сингулярного нестационарного разложения по собственным частотам ЭКС без патологии (а) и ЭКС с инверсным зубцом Т (б)
Литература
- Марпл.-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ.- М.: Мир, 1990.- 584 с.
- Дабровски А, Дабровски Б., Пиотрович Р. Суточное мониторирование ЭКГ – М.: Медпрактика, 2000. – 208 с.
- Техническая кибернетика. Теория автоматического регулирования. Книга 3. Часть 1 / Под ред. В.В. Солодовникова М.: 1969. 608 с.
- Гласс Леон, Мэки Майкл. От часов к хаосу: Ритмы жизни / Пер. с англ. Р.И. Сельковой; Под ред. Е.Е. Селькова. – М.: Мир, 1991. – 248 с.
Содержание конференции | Секция1
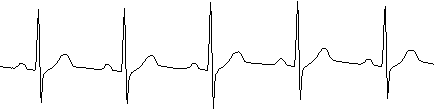
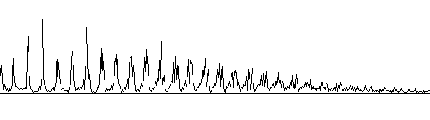 а)
а)
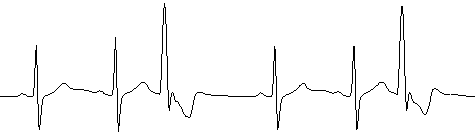
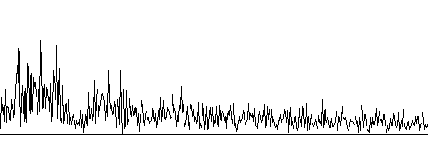 б)
б)
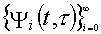
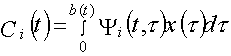 ,(1)
,(1)
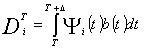 .(2)
.(2)

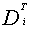 .
.


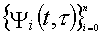 .
.
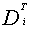 выбрать наиболее коррелированные ритмы. Очевидно, что наиболее коррелирован ритм сам с собой, поэтому в качестве нестационарных отрезков, на которых определяются спектральные коэффициенты, могут быть взяты отрезки, определяемые одним и тем же ведущим ритмом, назовем такое разложение сингулярным разложением по собственным ритмам в базисе нестационарных ортогональных функций
выбрать наиболее коррелированные ритмы. Очевидно, что наиболее коррелирован ритм сам с собой, поэтому в качестве нестационарных отрезков, на которых определяются спектральные коэффициенты, могут быть взяты отрезки, определяемые одним и тем же ведущим ритмом, назовем такое разложение сингулярным разложением по собственным ритмам в базисе нестационарных ортогональных функций
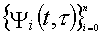 .
.