ИСПОЛЬЗОВАНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ В ПОСТРОЕНИИ МОДЕЛИ РАДИОЧАСТОТНОЙ АБЛАЦИИ СЕРДЦА

А.С. Кравчук, Р.В.Фатеенко

МГАПИ
Москва, ул. Стромынка, 20,
e-mail: roman4all@mail.ru

Радиочастотная аблация (РЧА) в настоящее время является основным методом радикальной коррекции сердечных аритмий и продолжает бурно развиваться. Большинство операций, производимых с использованием аппаратов искусственного кровообращения (ИК), были вытеснены на второй план с появлением этого метода, т.к. он является нетравматичным и малоинвазивным, несет за собой наименьшее количество осложнений, является высокоэффективным и позволяет сократить время пребывания пациента в стационаре до 2-3 суток.

В настоящей работе для решения проблемы подбора режимов внешних воздействий разработана математическая модель, основанная на уравнениях теплопроводности, потенциала дополнительных вытекающих из опыта гипотез.

1. Описание метода. Метод РЧА заключается в том, чтобы исключить влияние патологических путей проведения возбуждения по миокарду посредством воздействия электрического тока, интенсивность которого достаточна для появления необратимого некроза в очаге аритмии.

Первоначально проводится электрофизиологическое исследование (ЭФИ) с помощью диагностических электродов, проведенных через подключичные вены, что дает возможность выявить локализацию аритмогенного очага и классифицировать аритмию. Затем через вену или артерию, в зависимости от локализации, проводится управляемый катетер с аблационным электродом на конце, подсоединенный к радиочастотному генератору. Под спиной пациента размещают пассивный электрод, размер которого на много превышает диаметр контактного наконечника аблационного электрода.

При РЧА сердца используются частоты от 300 кГц до 1 МГц, иногда до 1,5 МГц. Все манипуляции с проведением и установкой катетеров происходят под рентгенологическим контролем.

Аблационный электрод диаметром не более 3 мм устанавливается в зону источника тахикардии и в этом месте наносится воздействие РЧ-током, приводя к нагреву ткани. При этом нагрев ткани в непосредственной близости от электрода происходит благодаря джоулевскому эффекту, в то время как в отдаленных участках температура увеличивается благодаря теплопроводности самой ткани. В тех участках, где ткань нагревается свыше 50°С, появляется необратимый некроз, электрический импеданс ткани резко возрастает, делая ее слабо проводимой, и тем самым, определяя границу объема поражения.

2. Постановка задачи. Основной задачей в планировании операции является формирование зоны поражения заданной формы, поскольку известно, что структура аритмогенной зоны сильно зависит от типа заболевания. В частности, установлено, что поражения тонкой удлиненной формы наиболее эффективны при лечении атриальной фибрилляции, в то время как глубокие и широкие поражения дают наибольший эффект при лечении мономорфных желудочковых тахикардий. Кроме того, во избежание обугливания и микроразрывов ткани чтобы температура ткани не должна достигать 100°С.

Из-за температурных градиентов внутри ткани термодатчики, помещаемые на контактной поверхности аблационного электрода, обычно не способны прецизионно контролировать наивысшую температуру ткани. Следовательно, необходимо выяснить, каковы распределения плотности тока и температуры в окрестности аблационного электрода. Кроме того, необходимо оценить, как отражается на степени эффективности аблации использование различных углов между аблационным электродом и поверхностью ткани, наличие кровотока и дополнительного охлаждения области аблации с помощью физиологического раствора, каково оптимальные величины мощности РЧ-тока и времени воздействия, расстояния между электродом и поверхностью ткани, размер и форма аблационного электрода.

Особую трудность вызывает измерение (с хорошим пространственным разрешением) действительных плотностей тока и температуры внутри ткани, расположенной в непосредственной близости к электроду. В связи с этим, а также по причине отсутствия общепринятой теоретической базы для данного вида терапии, возникла необходимость в создании модели процесса аблации ткани и в получении экспериментальных данных для определения оптимальной техники проведения операций и дальнейшего усовершенствования приборов и материалов, используемых при РЧА.

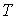3. Математическая модель. Математическая модель процесса аблации была построена с использованием следствий из законов термодинамики и уравнений Максвелла. В качестве переменных, определяющих состояние исследуемой системы были выбраны: температура в области 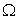, занятой биотканью, и электрический потенциал 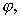определеяемый потенциалам ина приложенных к границе 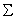области 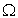электродах. В общем случае распределение температуры подчиняется уравнению теплопроводности:

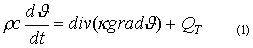
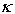где r- плотность, c - удельная теплоемкость, -теплопроводность, 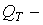плотность источников (стоков) тепла; 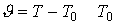- комнатная температура, 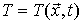- текущая температура, 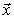- пространственные координаты, 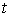- время. Символ 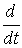означает полную производную по времени, равную сумме локальной скорости изменения и конвективной. Этот объект используется в том случае, когда учитываются большие перемещения сердечной мышцы во время операции, а также гидродинамика потока крови в крупных сосудах. К уравнению (1) присоединяются граничные условия, которые приближенно можно взять в форме условий Дирихле:

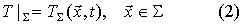
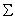где - граница области 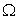, занятой исследуемым материалом (органом), в которой работает уравнение (1). Необходимо также задать начальное условие:

,

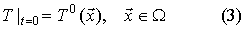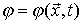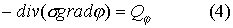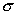определяющее начальное распределение температуры в теле.

Второе из основных уравнений – это уравнение для электрического потенциала

:

,

в котором - электрическая проводимость биоткани, в данной задаче зависящая от координат и времени, 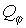- плотность распределенных в области электрических зарядов.

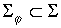К уравнению (4) необходимо добавить граничные условия, которые на части поверхности , к которой подсоединен задающий электрод, имеет вид:

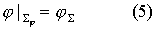
где - заданная функция координат и времени; на части поверхности 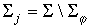задается условие отсутствия тока через границу:

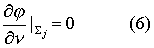
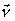производная слева в условии (6) – это производная по направлению единичной внешней нормали к границе 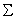. Система уравнений (10-(6) оказывается связанной, поскольку плотность тепловых источников 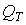в исследуемом процессе определяется главным образом возникновением джоулева тепла, т.е. зависит от искомой функции , входящей в уравнение (2). Если предположить, что не вся энергия электрического тока расходуется на нагревание, а только некоторая ее часть, пропорциональная джоулеву теплу, и что нельзя пренебречь переносом тепла вследствие кровотока, то:

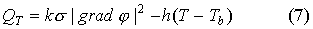
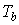где - температура крови, 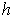- коэффициент теплопередачи. Часть генерируемой электрическим током тепловой энергии расходуется на коагуляцию биоткани, так что коэффициент 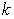в формуле (7) не превосходит единицы.

4. Дискретизация и метод решения. Поскольку исследуемая область – миокард с окружающими его тканями и потоком крови – имеет сложную форму, которая, зависит, очевидно, от конкретного пациента, то для дискретизации – перехода к конечно-мерной задаче наиболее подходящим представляется метод конечных элементов [1]. В соответствии с этим методом исследуемая область разбивается на конечное число подобластей, в каждой из которых искомые функции аппроксимируются полиномами степени не ниже первой. В результате система уравнений и соотношений (1) – (7) преобразуется в смешанную систему – частичной алгебраическую, соответствующую уравнению потенциала (4), частично – в систему обыкновенных дифференциальных уравнений, соответствующих уравнению теплопроводности (1). Для решения естественным является итерационный процесс, в котором сначала решается уравнение для потенциала при известной температуре, от которой может зависеть электрическая проводимость среды и распределение свободных зарядов. После этого решается уравнение теплопроводности (1), которое – как уже было отмечено – после дискретизации по методу конечных элементов преобразуется в систему обыкновенных дифференциальных уравнений первого порядка. Для решения возникающей здесь задачи Коши может быть применен известтный метод Рунге-Кутта.

Отметим, что длительность процесса аблации велика по сравнению с периодом колебаний электрического потенциала (минуты и микросекнды), в то же амплитуда колебаний температуры будет медленно возрастать с ростом времени. Для исключения возникающей здесь проблемы предлагается использовать асимптотический метод медленно меняющихся амплитуд или более общий метод осреднения [2].

Предложенная методика была реализована в виде программы для персонального компьютера. Численные результаты, полученные пока с использованием ряда упрощающих предположений (например, о постоянстве коэффициентов в уравнениях (1)-(7)), удовлетворительно согласуются с имеющимися в литературе [3], а также с некоторыми экспериментальными данными.

Литература
  1. Зенкевич О.С. Метод конечных элементов в технике. М.:Мир, 1975. 340с.
  2. Филатов А.Н. Методы усреднения в дифференциальных и интегро-дифференциальных уравнениях. Ташкент, ФАН, 1971. 279с.
  3. Panescu D., Whayne J.G., Fleischman S.D., Mirotznik M.S., Swanson D.K., Webster J.G. IEEE Trans. On Biomed. Engg. 1995, vol. 42, N 9, pp. 879-890.

Содержание конференции | Секция6